Answer:

Explanation:
To answer this question, you can use a number pattern that is well-known in algebra & higher mathematics called Pascal's Triangle. However, for simplification reasons, I will use the Binomial Theorem as it is quite difficult to create Pascal's Triangle without just attaching an image. A binomial is any two-term expression that are not like terms (for instance, both are integers that lack a variable).
Part I - Expanding the Binomial using the Binomial Theorem
After constructing Pascal's Triangle, you can use this method to expand a binomial. To do this, it will require a lot of patience and a lot of space.
Using Pascal's Triangle, we can expand the binomial entirely by referencing the exponents given and the coefficients that we have now solved for using Pascal's Triangle.
Referring to the seventh exponent row of the triangle, we can expand the binomial using a formula referred to as the Binomial Theorem.
The binomial theorem states that:
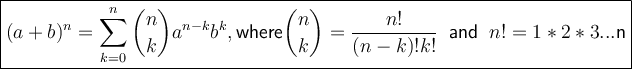
Therefore, we can use this information to begin defining values and expanding the binomial.
We are given an a, b, and n value. These are defined as a = 2y, b = x, and n = 7.
Therefore,
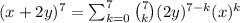 .
.
Using this information, you can then solve for every k-value. This will be slightly extensive. To solve for each k-value, ignore the summation sign and everything before it. You only need the information that follows the summation sign:
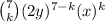 . This will then extend and allow you to only use the portions of the equation that require factorials.
. This will then extend and allow you to only use the portions of the equation that require factorials.
Be sure that when you get a final answer that you always apply the exponent (k) to the final result.
k = 0
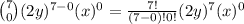
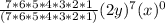
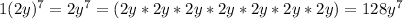
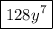
k = 1
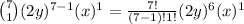
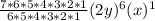
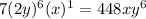
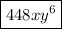
k = 2
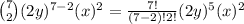
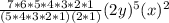
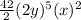
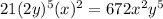
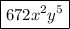
k = 3
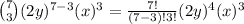
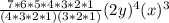
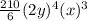
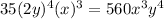
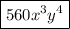
k = 4
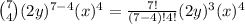
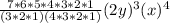

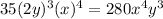
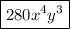
k = 5
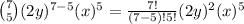
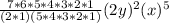

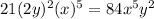
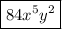
k = 6
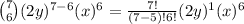
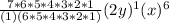
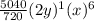

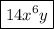
k = 7

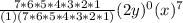


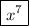
Part II - Adding/Subtracting all Terms Together
Now, we have to take a look at the original binomial and discover whether or not we are to add or subtract these terms together. The original binomial was
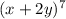 , so we will add (that is the operation of the binomial).
, so we will add (that is the operation of the binomial).
Therefore, we will add all of the terms that we started with following algebraic notation (that is, alphabetically and highest exponent to lowest exponent).

This is the final expanded binomial (now a polynomial).