We have been given that a Bowling ball is rolled down the alley with the constant velocity of 1.6 m/sec at an angle of 85° to the starting line, the position of the person throwing a bowling ball can be represented by the point (0,0).
We are asked to find the position of ball after 6 seconds.
We will use horizontal position and vertical position formula to solve our given problem.
Horizontal position is given by formula:
 and vertical position is given by formula:
and vertical position is given by formula:
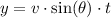 ,where,
,where,
v = Velocity,
t = Time,
 = Angle to the starting line.
= Angle to the starting line.
For our given problem
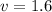 ,
,
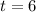 and
and
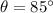 .
.

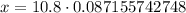
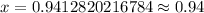
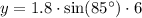

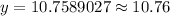
Therefore, the position of ball after 6 seconds would be
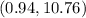 .
.