Verify the following identity. -(cos(3x)+cos(5x))/(sin(3x)-sin(5x))=cot(x)

Question

Verify the following identity.


`-(cos(3x)+cos(5x))/(sin(3x)-sin(5x))=cot(x)`

Answer 1

Recall the angle sum identities:

cos(a + b) = cos(a) cos(b) - sin(a) sin(b)

cos(a - b) = cos(a) cos(b) + sin(a) sin(b)

sin(a + b) = sin(a) cos(b) + sin(b) cos(a)

sin(a - b) = sin(a) cos(b) - sin(b) cos(a)

Notice that adding the first two together, and subtract the last from the third, we get two more identities:

cos(a + b) + cos(a - b) = 2 cos(a) cos(b)

sin(a + b) + sin(a - b) = 2 sin(b) cos(a)

Let a = 4x and b = x. Then

cos(5x) + cos(3x) = 2 cos(4x) cos(x)

sin(5x) - sin(3x) = 2 sin(x) cos(4x)

Now,

`-(\cos(3x)+\cos(5x))/(\sin(3x)-\sin(5x))=(\cos(5x)+\cos(3x))/(\sin(5x)-\sin(3x))=(2\cos(4x)\cos x)/(2\sin x\cos(4x))=(\cos x)/(\sin x)=\cot x`

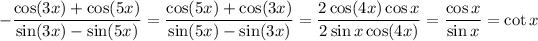
as required.