Answer:
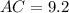
Explanation:
The Law of Sines states:
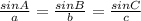
The lower case letters represent the sides opposite the angles: ∠A - side a, ∠B- side b, ∠C- side c. It helps to make a model.
To Find AC, or side b, we can use A and B because we have the appropriate information to solve for b. Insert values:
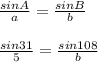
Solve for b. Multiply both sides by b:
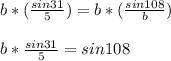
Multiply both sides by 5:
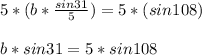
Divide both sides by sin 31:
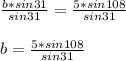
Enter the simplified equation into a calculator:
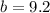
The length of AC is 9.2 units.
:Done