Answer:
The waves interfere destructively occur. The further explanation is given below.
Step-by-step explanation:
The transmissions almost commute with either the speed of light. So, use the following relation to calculate the wavelength of that same TV signal.
⇒ λ =
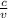
⇒ =
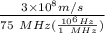
⇒ =
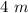
The variance in the route between both the 2 waves that approach the recipient is 248 m, also because wave passes 124 m two times. And then after the plane's reflective thinking the waves iteration adjustments by half.
⇒ Δ
 =
=
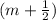 λ
λ
If the value of the above expression is a positive integer, the waves interfere constructively, as well as the waves disrupt destructively if they are integral multiples of the half. Caused by a change of step due to the reflection the component of half would be added.
⇒
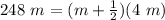
⇒
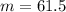
Since the value of m seems to be an integral multiple of the half.
Therefore, the waves interfere destructively