Question

The body mass index (BMI) of an individual is a measure used to judge whether or not an individual is overweight. A BMI between 20 and 25 indicated a normal weight. In a survey of 750 men and 750 women, the Gallup organization found that 203 men and 270 women were normal weight. Construct a 95% confidence interval for the difference in proportion of men and women who are normal weight.

Answer 1

Given Information:

Number of Men having normal weight = 203

Number of Women having normal weight = 270

Sample size of Men = 750

Sample size of Women = 750

Confidence level = 95%

Required Information:

Difference in the proportion of normal weighted Men and Women = ?

Answer:

We are 95% confident that the difference in the proportion of Men and Women who are normal weight is between (0.044, 0.136)

Explanation:

The proportion of Men who are normal weight is given by

p₁ = 203/750

p₁ = 0.27

The proportion of Women who are normal weight is given by

p₂ = 270/750

p₂ = 0.36

The difference in the proportion of normal weighted Men and Women is given by

`(p_2- p_1) \pm z\cdot \sqrt{(p_1(1-p_1))/(n_1) + (p_2(1-p_2))/(n_2)}`

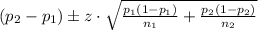
Where p₁ and p₂ are the proportion of Men and Women who are normal weighted.

n₁ and n₂ are the sample size of Men and Women.

z is the value of z-score corresponding to 95% confidence level and is given by

`z_(\alpha/2) = 1 - 0.95 = 0.05/2 = 0.025\\\\z_(0.025) = 1.96`

So we have z-score of 1.96 corresponding to confidence level of 95%

So the above equation becomes

`(p_2- p_1) \pm z\cdot \sqrt{(p_1(1-p_1))/(n_1) + (p_2(1-p_2))/(n_2)}\\\\(0.36- 0.27) \pm 1.96\cdot \sqrt{(0.27(1-0.27))/(750) + (0.36(1-0.36))/(750)}\\\\0.09\pm 1.96\cdot (0.0238) \\\\0.09\pm 0.046 \\\\Lower \: limit = 0.09 - 0.046 = 0.044\\\\Upper \: limit = 0.09 + 0.046 = 0.136\\\\(0.044, \: 0.136)`

Therefore, we are 95% confident that the difference in the proportion of Men and Women who are normal weight is between (0.044, 0.136)

How to find the value of z-score?

In the z-table find the probability of 0.025 and note down the value of that row it would be 1.9 and the value of column would be 0.06, therefore, the z-score is 1.9+0.06 = 1.96