Given Information:
Number of Men having normal weight = 203
Number of Women having normal weight = 270
Sample size of Men = 750
Sample size of Women = 750
Confidence level = 95%
Required Information:
Difference in the proportion of normal weighted Men and Women = ?
Answer:
We are 95% confident that the difference in the proportion of Men and Women who are normal weight is between (0.044, 0.136)
Explanation:
The proportion of Men who are normal weight is given by
p₁ = 203/750
p₁ = 0.27
The proportion of Women who are normal weight is given by
p₂ = 270/750
p₂ = 0.36
The difference in the proportion of normal weighted Men and Women is given by
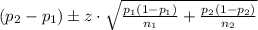
Where p₁ and p₂ are the proportion of Men and Women who are normal weighted.
n₁ and n₂ are the sample size of Men and Women.
z is the value of z-score corresponding to 95% confidence level and is given by
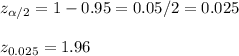
So we have z-score of 1.96 corresponding to confidence level of 95%
So the above equation becomes

Therefore, we are 95% confident that the difference in the proportion of Men and Women who are normal weight is between (0.044, 0.136)
How to find the value of z-score?
In the z-table find the probability of 0.025 and note down the value of that row it would be 1.9 and the value of column would be 0.06, therefore, the z-score is 1.9+0.06 = 1.96