Answer:
C. It will increase by about 0.6%
Step-by-step explanation:
Since, the effective interest rate is,
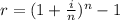
Where, i is the stated interest rate,
n is the number of compounding periods,
Here, i = 11.28 % = 0.1128,
n = 365 ( 1 year = 365 days ),
Hence, the effective interest rate would be,
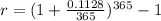
=0.119388521952
Now, the changes in effective interest rate = Effective interest rate - Stated interest rate
= 0.119388521952 - 0.1128
= 0.006588521952 ≈ 0.006 = 0.6 %
Hence, It will increased by about 0.6 %,
Option A is correct.
Hope this helps :)