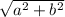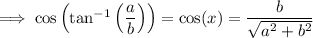Question

I can’t solve this can someone help me

Answer 1

`\textsf{D.}\quad(b)/(√(a^2+b^2))`

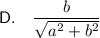
Explanation:

Tan trig ratio

`\tan(x)=\sf (O)/(A)`

where:

• 
  `x` is the angle
• O is the side opposite the angle
• A is the side adjacent the angle

Using the given information:

`\implies x=\tan^(-1)\left((a)/(b)\right)`

`\implies \tan(x)=\tan\left(\tan^(-1)\left((a)/(b)\right)\right)`

`\implies \tan(x)=\left((a)/(b)\right)`

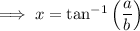
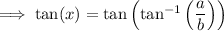
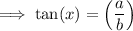
Comparing this with the trig ratio, we can say that:

`x` is the angle opposite side
`a`

Cos trig ratio

`\cos(x)=\sf (A)/(H)`

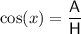
where:

• 
  `x` is the angle
• A is the side adjacent the angle
• H is the hypotenuse

Therefore:

• A = side
  `b`
• H = side
  `√(a^2+b^2)`

`\implies \cos\left(\tan^(-1)\left((a)/(b)\right)\right)=\cos(x)= (b)/(√(a^2+b^2))`