Answer:
26.92 N
Step-by-step explanation:
The normal reaction of the ball is due to two force component acting on it.
- The normal reaction as a result of the weight of the ball
- The normal reaction due to the component of the acceleration of the ball with the rod.
However ; the acceleration is in polar coordinate which is given by the relation:
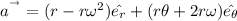
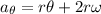
Given that :
ω = 5 rad/s
mass m = 6 kg
θ = 30 ◦
r = 0.9 m
speed v = 0.4 m/s
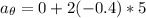
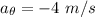
The normal force reaction (N) that the arm applies to the ball at this instant is :
N = mg cos θ +
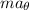
N = (6 × 9.8× cos 30) + (6 ×(-4))
N = 26.92 N