Question

A 200.0 g block rests on a frictionless, horizontal surface. It is pressed against a horizontal spring with spring constant 4500.0 N/m (assume that the spring is massless). The block is held in position such that the spring is compressed 4.00 cm shorter than its undisturbed length. The block is suddenly released and allowed to slide away on the frictionless surface. Find the speed the block will be traveling when it leaves the spring.

Answer 1

6 m/s

Step-by-step explanation:

Given that :

mass of the block m = 200.0 g = 200 × 10⁻³ kg

the horizontal spring constant k = 4500.0 N/m

position of the block (distance x) = 4.00 cm = 0.04 m

To determine the speed the block will be traveling when it leaves the spring; we applying the work done on the spring as it is stretched (or compressed) with the kinetic energy.

i.e
`(1)/(2) kx^2 = (1)/(2) mv^2`

`kx^2 = mv^2`

`4500* 0.04^2 = 200*10^(-3) *v^2`

`7.2 =200*10^(-3)*v^(2)`

`v^(2) =(7.2)/(200*10^(-3))`

`v =\sqrt{(7.2)/(200*10^(-3))}`

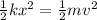
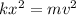
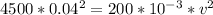
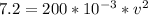
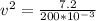
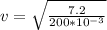
v = 6 m/s

Hence,the speed the block will be traveling when it leaves the spring is 6 m/s