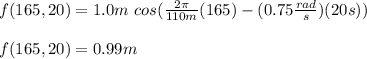Question

A"boat"is"moving"to"the"right"at"5"m/s"with"respect"to"the"water."A"wave"moving"to"the"left,"opposite"the"motion"of"the"boat."The"waves"have"2.0"m"between"the"top"of"the"crests"and"the"bottom"of"the"troughs."The"period"of"the"wave"is"8.3"s"and"their"wavelength"is"110"m."At"one"instant"the"boat"sits"on"a"crest"of"the"wave,"20"seconds"later,"what"is"the"vertical"displacement"of"the"boat

Answer 1

0.99m

Step-by-step explanation:

Firs you calculate the relative velocity between the boat and the wave. The velocity of the boat is 5m/s and the velocity of the wave is given by:

`v=\lambda f=\lambda(1)/(T)=(110m)(1)/(8.3s)=13.25(m)/(s)`

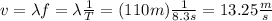
the relative velocity is:

`v'=13.25m/s-5m/s=8.25(m)/(s)`

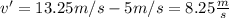
This velocity is used to know which is the distance traveled by the boat after 20 seconds:

`x'=v't=(8.25m/s)(20s)=165m`

Next, you use the general for of a wave:

`f(x,t)=Acos(kx-\omega t)=Acos((2\pi)/(\lambda)x-\omega t)`

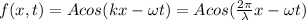
you take the amplitude as 2.0/2 = 1.0m.

`\omega=(2\pi)/(T)=(2\pi)/(8.3s)=0.75(rad)/(s)`

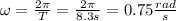
by replacing the values of the parameters in f(x,t) you obtain the vertical displacement of the boat:

`f(165,20)=1.0m\ cos((2\pi)/(110m)(165)-(0.75(rad)/(s))(20s))\\\\f(165,20)=0.99m`