Answer:
a)
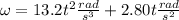
b)
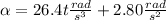
Step-by-step explanation:
You have that the angular displacement is given by:
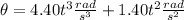
a) the angular velocity is given by the derivative in time, of the angular displacement, that is:
![\omega=(d\theta)/(dt)=(d)/(dt)[4.40 t^3 rad/s^3 + 1.40 t^2 rad/s^2]\\\\\omega=(d\theta)/(dt)=13.2t^2(rad)/(s^3)+2.80t(rad)/(s^2)](https://img.qammunity.org/2021/formulas/physics/college/iyto2elms40re9lo22u3vf6wgb0ssfwbbr.png)
b) the angular acceleration is the derivative, in time, of the angular velocity:
![\alpha=(d\omega)/(dt)=(d)/(dt)[13.2t^2(rad)/(s^3)+2.80t(rad)/(s^2)]\\\\\alpha=26.4t(rad)/(s^3)+2.80(rad)/(s^2)](https://img.qammunity.org/2021/formulas/physics/college/yt3orrppdp08xakk8wxmkajjvho93l6x7v.png)