Answer:
$220,000 represents the initial cost of a real estate that appreciates 3% per year over the course of t years.
Explanation:
Equation for a real estate value:

Where V(t) represents the value of the real estate
t represents the time in years.
Exponential growth equation:
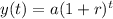
Exponential decay equation:
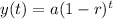
The given Equation for a real estate value can be written as :
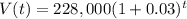
Om comparing with growth and decay equations
We conclude that it is the growth equation
Where r = 0.03 =3%
a=Initial cost = 228000
So, Option B is true
$220,000 represents the initial cost of a real estate that appreciates 3% per year over the course of t years.