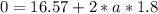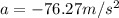Answer:
The deceleration is
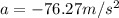
Step-by-step explanation:
From the question we are told that
The height above firefighter safety net is
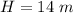
The length by which the net is stretched is
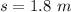
From the law of energy conservation
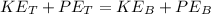
Where
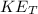 is the kinetic energy of the person before jumping which equal to zero(because to kinetic energy at maximum height )
is the kinetic energy of the person before jumping which equal to zero(because to kinetic energy at maximum height )
and
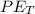 is the potential energy of the before jumping which is mathematically represented at
is the potential energy of the before jumping which is mathematically represented at
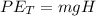
and
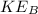 is the kinetic energy of the person just before landing on the safety net which is mathematically represented at
is the kinetic energy of the person just before landing on the safety net which is mathematically represented at

and
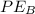 is the potential energy of the person as he lands on the safety net which has a value of zero (because it is converted to kinetic energy )
is the potential energy of the person as he lands on the safety net which has a value of zero (because it is converted to kinetic energy )
So the above equation becomes
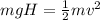
=>
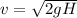
substituting values
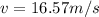
Applying the equation o motion
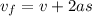
Now the final velocity is zero because the person comes to rest
So