Question

Help 80 points A concrete planter is formed from a square-based pyramid that was inverted and placed

inside a cube.

A. What is the slant height of the pyramid?

B. What is the surface area of the composite figure?

HINT: The surface area consists of lateral faces of the

inside of the inverted pyramid and the remaining 5

faces of the cube.

C. How many cubic yards of concrete are needed to make the planter?

Answer 1

(A)

The slant height of the pyramid refers to the height of a face of the pyramid.

Notice that each slant height forms a right triangle like the image attached shows, where the hypothenuse is the slant height. Additionally, the bottom leg is 1 yard, because is half of the base side, and the other leg is 2 yard. Using Pythagorean's Theorem, we have

`h^(2) =1^(2) +2^(2) \\h=√(1+4)=√(5)`

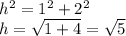
Therefore, the slant height is the square root of 5 yard.

(B)

The surface area of the composite figure is the sum of the surface area of both volumes.

Surface area of the cube.

`S_(cube)=5(2yd)^(2) =20 yd^(2)`

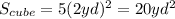
Notice that we only included 5 faces of the cube, that is because the sixth is the base of the pyramid, so if we include it here, we would have the wrong total surface area.

Surface area of the pyramid.

`S_(pyramid)=(1)/(2)pl`

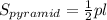
Where
`p` is the perimeter of the base and
`l` is the slant height.

`S_(pyramid)=(1)/(2)(8yd)(√(5)yd )=4√(5)yd ^(2)`

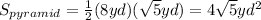
Therefore, the surface od the composite figure is

`S_(total)=20yd^(2) +4√(5) yd^(2) \approx 29.94 yd^(2)`

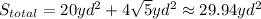
(C)

To find the cubic yards of concrete, we need to subtract the volume of the figures, because the concrete would be inside the space between the cube and the pyramid.

`V_(concrete)=V_(cube) -V_(pyramid)=l^(3)- (1)/(3)l^(2)h`

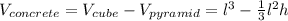
Where
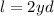`l=2yd` and
`h=2yd`

`V_(concrete)=2^(3)-(1)/(3)(2)^(2) (2)=8-(8)/(3) \approx 5.33 yd^(3)`

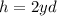
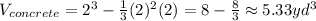
Therefore, it would be needed 5.33 cubic yards of concrete to make the planter.