Question

Direct mail advertisers send solicitations​ ("junk mail") to thousands of potential customers in the hope that some will buy the​ company's product. The response rate is usually quite low. Suppose a company wants to test the response to a new flyer and sends it to 1030 people randomly selected from their mailing list of over​ 200,000 people. They get orders from 103 of the recipients.

Required:
Create a 95% confidence interval for the percentage of people the company contacts who may buy something. (Show your work. Step by step)

Answer 1

The interval is (.0817, .118).

Explanation:

Let's make this interval! The easy way is to go to STAT->TEST->A, 1-prop z-int, but I will show the long way.

1. Conditions

First we must check the conditions.

Randomization condition: The sample is given to be random, so we can assume independence.

Success/failure condition: Both np>10 and nq>10 must be met.

• np = 1030(103/1030) = 103 ✓
• nq = 1030(927/1030) = 927 ✓

10% condition: The sample cannot be greater than 10% of the population.

• 10n < N, 10(1030) < 200000 ✓

All conditions are met, so we can use a 1-proportion z-interval to represent the data.

2. Mechanics

Find
`\hat{p}`, the sample proportion.

103/1030 = .1

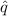`\hat{q}`, then, the probability of not p, is 1 - .1 = .9

Find z* (z star), the critical z-value.

You can do this on your calculator using 2nd->VARS->3 (or you can memorize it - it's 1.96. Winky face.) This is called the invNorm function, that takes the left side area under the normal curve. But what do we plug in to the invNorm function?

invNorm(.975) = 1.96

Plug values into the equation.

`\hat{p}` ± z*
`\sqrt{\frac{\hat{p}\hat{q}}{n} }`

.1 ± 1.96
`\sqrt{(.1*.9)/(1030) }`

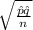
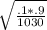
.1 ± 1.96(.00935)

.1 - .0183 = .0817

.1 + .0183 = .118

(.0817, .118)

3. Conclusion

Based on this sample, we are 95% confident that the proportion of people the company contacts who may buy something is between .0817 and .118. That isn't very likely, but maybe they'll make a little profit!