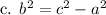Question

A right triangle has side lengths of a, b, and cunits. The longest side has a length

of c units. Complete each equation to show three relations among a, b, and c.
a. c² =
b. a^2=
c. 6² =

Answer 1

`\text{a. }c^(2) = a^(2) + b^(2)`

`\text{b. }a^(2) = c^(2) - b^(2)`

`\text{c. }b^(2) = c^(2) - a^(2)`

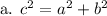
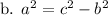
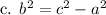
Explanation:

Please refer to the attached figure in which
`\triangle ABC` is shown with sides a, b and c.

It is given a right angled triangle with sides a, b and c.

And c is the longest side.

So, it is clear that 'c' is the hypotenuse of the triangle because hypotenuse is the longest side of a right angled triangle.

No condition is given about the base and height.

So, let 'a' be the height and 'b' be the base of triangle as shown in the attached figure in the answer area.

We know that, pythagoras' theorem holds true in every right angled triangle.

According to pythagoras' theorem:

`Hypotenuse^(2) = Base^(2) + Height^(2)\\\Rightarrow c^(2) = a^(2) + b^(2) .......... (1)`

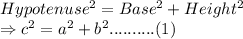
So, Answer
`\text{a. }c^(2) = a^(2) + b^(2)`

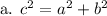
Using equation(1):

Answer
`\text{b. }a^(2) = c^(2) - b^(2)`

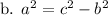
Also,

Answer
`\text{c. }b^(2) = c^(2) - a^(2)`