Question

2. Find out the enthalpy change of the CH4 from solid Carbon and Hydrogen gas. C (s)+ 2H2 (g)(CH4(g) (H( = ?

Use the following three equations:
C (s)+ O2 (g)(CO2(g) (H( = -393.5 kJ
H2 (g)+1/2 O2 (g)(H2O(l) (H( = -285.8 kJ
CH4 (g)+ 2O2 (g)( CO2(g)+ 2H2O(l) (H( = -890.3 kJ

Answer 1

Approximately
`-74.8\; \rm kJ \cdot mol^(-1)`.

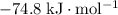Step-by-step explanation:

Number the three reactions with known enthalpy changes:

`\begin{aligned}& {\rm C\; (s) + O_2\; (g) \to CO_2\; (g)} & \quad \Delta H = -393.5\; \rm kJ\cdot mol^(-1)& \quad (1) \\ & {\rm H_2\; (2) + (1)/(2) O_2\; (g) \to H_2O\; (l)} & \quad \Delta H = -285.8\; \rm kJ\cdot mol^(-1) & \quad (2) \\ & {\rm CH_4\; (g) + 2\; O_2\; (g) \to CO_2\; (g) + 2\; H_2O\; (l)} & \quad \Delta H = -890.3\; \rm kJ\cdot mol^(-1) & \quad (3)\end{aligned}`.

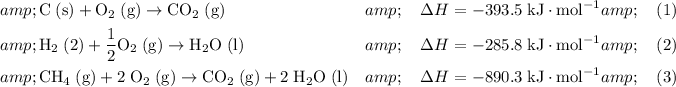The goal is to find a way to combine these three reactions to obtain:
`\rm C\; (s) + 2\; H_2\; (g) \to CH_4\; (g)`.

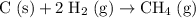Assume that the three known reactions are combined in this way:

`a * (1) + b * (2) + c * (3)`.

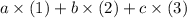That corresponds to:

`\begin{aligned} & a\; \mathrm{C\; (s)} + \left(a + (1)/(2)\, b + c\right) \; \mathrm{O_2\; (g)} + b\; \mathrm{H_2\; (g)} + c\; \mathrm{CH_4\; (g)} \\ & \to (a + c)\; \mathrm{CO_2\; (g)} + (b+ 2\,c )\; \mathrm{H_2O\; (l)}\end{aligned}`.

Compare the coefficients of this reaction with that of the desired reaction:

`\rm C\; (s) + 2\; H_2\; (g) \to CH_4\; (g)`.

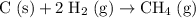Note that some species (e.g.,
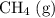`\rm CH_4\; (g)`) appeared on the wrong side of the equation. Their desired coefficient should be the opposite of their true coefficient. For example, the coefficient of
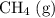`\rm CH_4\; (g)` is supposed to be
`1`. However, because it appeared on the wrong side of the equation, its desired coefficient would be
`-1`.

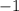The coefficients of species that are not in the desired equation should be zero.

`\begin{array}c\cline{1-3}\text{Species} & \text{Coefficient}& \text{Desired Coefficient} \\ \cline{1-3} \mathrm{C\; (s)}} & a & 1 \\ \cline{1-3} \mathrm{O_2\; (g)} & a + (1/2)\, b + c & 0 \\ \cline{1-3} \mathrm{H_2\; (g)} & b & 2 \\ \cline{1-3}\mathrm{CH_4\; (g)} & c & -1\\ \cline{1-3} \mathrm{CO_2\; (g)} & a + c & 0 \\ \cline{1-3} \mathrm{H_2O\; (l)} & b + 2\, c & 0\\ \cline{1-3}\end{array}`.

Solve for
`a`,
`b`, and
`c`:

• 
  `a = 1`.
• 
  `b = 2`.
• 
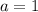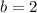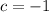  `c = -1`. In other words, the third equation is inverted before being added to the other two equations.

In other words, the desired equation is equal to
`1 * (1) + 2 * (2) - 1 * (3)`.

By Hess's Law, the enthalpy of the desired equation will be:

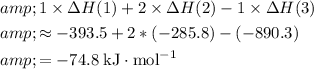`\begin{aligned}& 1* \Delta H (1) + 2 * \Delta H (2) - 1* \Delta H(3) \\ &\approx -393.5 + 2 * (-285.8) - (-890.3) \\ &= -74.8\; \rm kJ \cdot mol^(-1) \end{aligned}`.