Answer:
Approximately
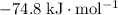 .
.
Step-by-step explanation:
Number the three reactions with known enthalpy changes:
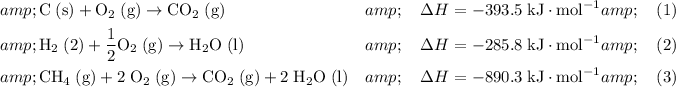 .
.
The goal is to find a way to combine these three reactions to obtain:
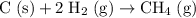 .
.
Assume that the three known reactions are combined in this way:
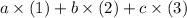 .
.
That corresponds to:
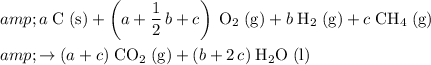 .
.
Compare the coefficients of this reaction with that of the desired reaction:
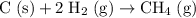 .
.
Note that some species (e.g.,
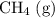 ) appeared on the wrong side of the equation. Their desired coefficient should be the opposite of their true coefficient. For example, the coefficient of
) appeared on the wrong side of the equation. Their desired coefficient should be the opposite of their true coefficient. For example, the coefficient of
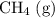 is supposed to be
is supposed to be
 . However, because it appeared on the wrong side of the equation, its desired coefficient would be
. However, because it appeared on the wrong side of the equation, its desired coefficient would be
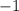 .
.
The coefficients of species that are not in the desired equation should be zero.
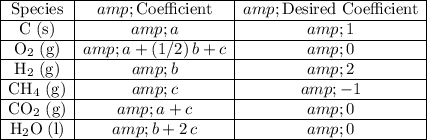 .
.
Solve for
 ,
,
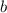 , and
, and
 :
:
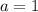 .
.
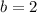 .
.
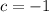 . In other words, the third equation is inverted before being added to the other two equations.
. In other words, the third equation is inverted before being added to the other two equations.
In other words, the desired equation is equal to
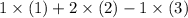 .
.
By Hess's Law, the enthalpy of the desired equation will be:
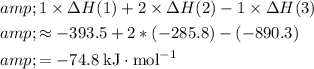 .
.