Answer:
The volume of the kaleidoscope (hollow cylinder) is 613.33 in.³
Explanation:
Here we have;
The equation for the volume of a cylinder given as follows;
Volume of cylinder = π × r² × h
Given that the height, h of the cylinder = 9 cm
The radius, r = 5 cm
Volume of the solid cylinder before cutting out the hexagon hole is thus found as follows;
Volume of cylinder = π × 5² × 9 = 706.86 cm³
Volume of hexagon hole = Area of base × height
Where:
Area, A of a regular hexagon of side a =
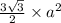
Therefore, volume of the regular hexagon =
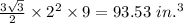
Therefore, the volume of the kaleidoscope (hollow cylinder) = 706.86 - 93.53 = 613.33 in.³.