Question

Determine the vertices, asymptotes, and foci of the hyperbola
`576x^2 - 16y^2=144`

Please show all your work - thanks! :)

Answer 1

The vertices are (±1/2, 0), the asymptote is y = -6x, and the foci of the hyperbola is

How to determine the vertices, asymptotes, and the foci?

The equation of the hyperbola is given as:

`576x^2 - 16y^2 = 144`

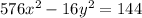
Divide through by 144

`4x2 - 9y2 = 1`

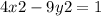
Rewrite as:

`2x 1/4 - y2 32 = 1`

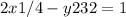
Hence, the vertices are (±1/2, 0), the asymptote is y = -6x, and the foci of the hyperbola is ⁽₍₋₋₂₋₋ ₃₇ ° 0₎⁾ Hope This helps Have A Nice Day!

Answer 2

Hyperbola Foci:
`\displaystyle (\pm (√(37))/(2), 0)`

Hyperbola Vertices:
`\displaystyle (\pm (1)/(2), 0)`

Hyperbola Asymptotes:
`\displaystyle y = \pm 6x`

General Formulas and Concepts:

Math

• Simplifying

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

• Coordinates (x, y)

Pre-Calculus

Hyperbola Standard Form:
`\displaystyle ((x - h)^2)/(a^2) - ((y - k)^2)/(b^2) = 1`

• Center (h, k)
• Hyperbola Vertices: (±a, 0)
• Hyperbola Foci: c² = a² + b²

Hyperbola Asymptotes:
`\displaystyle (y - k) = \pm (b)/(a)(x - h)`

Explanation:

Step 1: Define

`\displaystyle 576x^2 - 16y^2 = 144`

Step 2: Rewrite

Rewrite equation into hyperbola standard form

1. [Hyperbola] [Division Property of Equality] Divide 144 on both sides:
   `\displaystyle (576x^2 - 16y^2)/(144) = 1`
2. [Hyperbola] Split fraction:
   `\displaystyle (576x^2)/(144) - (16y^2)/(144) = 1`
3. [Hyperbola] Simplify:
   `\displaystyle 4x^2 - (y^2)/(9) = 1`
4. [Hyperbola] Rewrite:
   `\displaystyle (x^2)/((1)/(4)) - (y^2)/(9) = 1`
5. [Hyperbola] Rewrite a and b:
   `\displaystyle (x^2)/(((1)/(2))^2) - (y^2)/(3^2) = 1`

Step 3: Identify Parts

Compare the general standard form and our equation standard form to identify parts of the hyperbola.

`\displaystyle (x^2)/(((1)/(2))^2) - (y^2)/(3^2) = 1` ↔
`\displaystyle ((x - h)^2)/(a^2) - ((y - k)^2)/(b^2) = 1`

Hyperbola Center: (0, 0)

Hyperbola Vertices:
`\displaystyle (\pm (1)/(2), 0)`

Step 4: Identify Other Parts

We go slightly more complex in determining the asymptotes and foci of the hyperbola.

Foci

1. Substitute in variables [Hyperbola Foci]:
   `\displaystyle c^2 = ((1)/(2))^2 + 3^2`
2. [Hyperbola Foci] Evaluate exponents:
   `\displaystyle c^2 = (1)/(4) + 9`
3. [Hyperbola Foci] Add:
   `\displaystyle c^2 = (37)/(4)`
4. [Hyperbola Foci] [Equality Property] Square root both sides:
   `\displaystyle c = \pm \sqrt{(37)/(4)}`
5. [Hyperbola Foci] Simplify:
   `\displaystyle c = \pm (√(37))/(2)`

Our hyperbola foci are
`\displaystyle ((√(37))/(2), 0)` and
`\displaystyle (-(√(37))/(2), 0)`.

Asymptotes

1. Substitute in variables [Hyperbola Asymptotes]:
   `\displaystyle (y - 0) = \pm (3)/((1)/(2))(x - 0)`
2. [Hyperbola Asymptotes] (Parenthesis) Subtract:
   `\displaystyle y = \pm (3)/((1)/(2))x`
3. [Hyperbola Asymptotes] Divide:
   `\displaystyle y = \pm 6x`

Our hyperbola asymptotes are y = 6x and y = -6x.