Question

What are the measures of the angles in triangle ABC?

m∠A ≈ 46.2°, m∠B ≈ 43.8°, m∠C ≈ 90°

m∠A ≈ 73.0°, m∠B ≈ 17.0°, m∠C ≈ 90°

m∠A ≈ 73.7°, m∠B ≈ 16.3°, m∠C ≈ 90°

m∠A ≈ 74.4°, m∠B ≈ 15.6°, m∠C ≈ 90°

Answer 1

c

Explanation:

Answer 2

Complete question :

A right triangle has side lengths AC = 7 inches, BC = 24 inches, and AB = 25 inches.

What are the measures of the angles in triangle ABC?

a) m∠A ≈ 46.2°, m∠B ≈ 43.8°, m∠C ≈ 90°

b) m∠A ≈ 73.0°, m∠B ≈ 17.0°, m∠C ≈ 90°

c) m∠A ≈ 73.7°, m∠B ≈ 16.3°, m∠C ≈ 90°

d) m∠A ≈ 74.4°, m∠B ≈ 15.6°, m∠C ≈ 90°

Answer:

c) m∠A ≈ 73.7°, m∠B ≈ 16.3°, m∠C ≈ 90°

Explanation:

Given:

Length AC = 7 inches

Length BC = 24 inches

Length AB = 25 inches

Since it is a right angle triangle,

m∠C = 90°

To find the measures of the angle in ∠A and ∠B, we have :

For ∠A:

`SinA = (BC)/(AB)`

`SinA = (24)/(25)`

`SinA = 0.96`

`A = Sin^-^1 = 0.96`

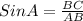
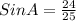
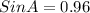
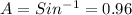
∠A = 73.7°

For ∠B:

`SinB = (AC)/(AB)`

`SinB = (7)/(25)`

`SinB = 0.28`

`B = Sin^-^1 = 0.96`

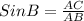
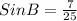
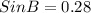
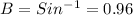
∠B = 16.26 ≈ 16.3°

Therefore,

m∠A = 73.7°

m∠B = 16.3°

m∠C = 90°