Answer:
The minimum length of the vertical curve that can be used is 416.63 m
Step-by-step explanation:
g₁ = -1.2% , g₂ = 0.8%
Station (Sta) = 75 + 00
Elevation (Ele) = 50.90 m
x₀ = Sta(VPC) = Sta(VPI) - L/2 ⇒ 7500 - L/2
y₀ = Ele(VPC) = Ele(VPI) - g₁L/2 == 50.90 - (-0.012)L/2 ⇒ 50.90 + 0.012L/2
at Sta 75+40, x = 7540 -x₀ = 40 + L/2
at Ele, y = 51.10 + C = 51.10 + 0.80 ⇒ y = 51.90 m
Equation of vertical curve is
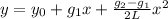
Substituting the values for x and y
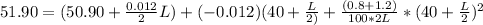
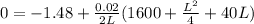
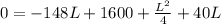
Solving : L = 416.63 m