Question

1. A vertical curve joins a -1.2% grade to a +0.8% grade. The two grades intersect at station 75 + 00 and elevation 50.90 m above sea level. The centerline of the roadway must clear a pipe located at station 75 + 40 by 0.80 m. The elevation of the top of the pipe is 51.10 m above sea level. What is the minimum length of the vertical curve that can be used?

Answer 1

The minimum length of the vertical curve that can be used is 416.63 m

Step-by-step explanation:

g₁ = -1.2% , g₂ = 0.8%

Station (Sta) = 75 + 00

Elevation (Ele) = 50.90 m

x₀ = Sta(VPC) = Sta(VPI) - L/2 ⇒ 7500 - L/2

y₀ = Ele(VPC) = Ele(VPI) - g₁L/2 == 50.90 - (-0.012)L/2 ⇒ 50.90 + 0.012L/2

at Sta 75+40, x = 7540 -x₀ = 40 + L/2

at Ele, y = 51.10 + C = 51.10 + 0.80 ⇒ y = 51.90 m

Equation of vertical curve is

`y = y_0 + g_1x + (g_2-g_1)/(2L)x^2`

Substituting the values for x and y

`51.90 = (50.90 + (0.012)/(2)L)+(-0.012)(40+(L)/(2))+((0.8+1.2))/(100*2L)*(40+(L)/(2))^2`

`0 = -1.48 + (0.02)/(2L)(1600+(L^2)/(4)+40L)`

`0 = -148L + 1600 + (L^2)/(4) + 40L`

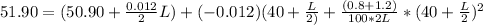
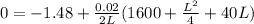
Solving : L = 416.63 m