By definition of linear independence, the vectors in the set {a, b, c} are independent if
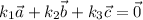
can only be obtained with the choice of k₁ = k₂ = k₃ = 0.
This vector equation corresponds to the system of linear equations
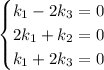
The first equation says k₁ = 2 k₃, while the third one says k₁ = -2 k₃. This can only be possible if k₁ = k₃ = 0, and from the second equation it follows that k₂ = 0. So the given set is linearly independent (and *not* dependent).