Answer:
Explanation:
Let a,b be vectors. Then we know that a and b are orthogonal if
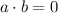 , where
, where
 is the dot product. We also say that if
is the dot product. We also say that if
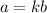 for some positive scalar k, when a and b are in the same direction. If k is negative, then a and b are in opposite directions.
for some positive scalar k, when a and b are in the same direction. If k is negative, then a and b are in opposite directions.
Note that c = -1*v. So c and v are in opposite directions. Also, note that w=3*u. so w and u are in the same direction. Note that since b=(0,1) and the others vectors have non-zero entries, this implies that none of the vectors are in the same direction nor opposite direction of b, given that 0 times any number is 0.
Note that
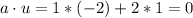 so a and u are orthogonal. Since w is in the direction of u, this implies that a is orthogonal to w. We also have that v = 2a. So v is in the same direction of a. Hence, v is orthogonal to u and w.
so a and u are orthogonal. Since w is in the direction of u, this implies that a is orthogonal to w. We also have that v = 2a. So v is in the same direction of a. Hence, v is orthogonal to u and w.
Finally, note that
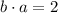 ,
,
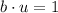 . So this implies that b is not orthogonal to any other vector in particular.
. So this implies that b is not orthogonal to any other vector in particular.