Question

Which of the vectors a = (1,2), b = (0,1), c = (−2,−4), u = (−2,1) , v = (2,4), w = (−6,3) are:

Orthogonal?

In the same direction?

In opposite directions?

Answer 1

(make sure you have a vector symbol above your vectors*)

orthog same opposite

a,u a,v a,v

a,w u,w u,w

c,u

c,w

u,v

v,w

Explanation:

To find Orthogonal vectors, check if the dot product is equal to zero

ex: vectors a and u are orthogonal

`(1*-2)+(2*1)\\=-2+2\\=0`

To find same direction vectors, look for vectors that are scaled versions of other vectors

ex: vectors a and v are same direction

2(a)=v 2(1,2)=(2,4)

Opposite direction vectors are just the negative versions of other vectors (scaled by a negative number)

ex: vectors a and c are opposite

-2(a)=c -2(1,2)=(-2,-4)

*If you are coming from RSM:

To enter your answers, first, enter a ray symbol

(a depiction is attached)

Answer 2

Explanation:

Let a,b be vectors. Then we know that a and b are orthogonal if
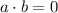`a\cdot b =0`, where
`\cdot` is the dot product. We also say that if

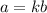`a= kb` for some positive scalar k, when a and b are in the same direction. If k is negative, then a and b are in opposite directions.

Note that c = -1*v. So c and v are in opposite directions. Also, note that w=3*u. so w and u are in the same direction. Note that since b=(0,1) and the others vectors have non-zero entries, this implies that none of the vectors are in the same direction nor opposite direction of b, given that 0 times any number is 0.

Note that
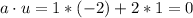`a\cdot u = 1*(-2)+2*1 =0` so a and u are orthogonal. Since w is in the direction of u, this implies that a is orthogonal to w. We also have that v = 2a. So v is in the same direction of a. Hence, v is orthogonal to u and w.

Finally, note that
`b\cdot a = 2` ,
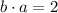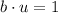`b\cdot u = 1`. So this implies that b is not orthogonal to any other vector in particular.