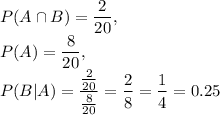Question

Given that a randomly chosen quadrilateral has four right

angles, what is the probability that the quadrilateral also

has four equal side lengths? Express your answer in

percent form, rounded to the nearest whole percent.

hose

Answer 1

a.25%

Explanation:

edg 2021

Answer 2

0.25

Explanation:

complete question:

Bart found 20 quadrilaterals in his classroom. He made a Venn diagram using the properties of the quadrilaterals, comparing those with four equal side lengths (E) and those with four right angles (R).

See attachment for the figure.

SOLUTION:

At Venn diagram there are 4 parts (20 pieces):

-> blue colored - quadrilaterals having four equal side lengths (3 pieces)

-> orange colored - quadrilaterals with four right angles (6 pieces)

-> blue and orange colored - quadrilaterals with four right angles and with four equal side lengths (2 pieces)

-> white colored - quadrilaterals without previous two properties (9 pieces).

Considering events:

A -> a randomly chosen quadrilateral has four right angles;

B -> a randomly chosen quadrilateral has four equal side lengths;

By using formula :
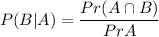`P(B|A)=(Pr(A\cap B))/(Pr A)` in order to find probability that a randomly selected quadrilateral with 4 right angles also has four equal side lengths:

`P(A\cap B)=(2)/(20),\\P(A)=(8)/(20),\\P(B|A)=((2)/(20))/((8)/(20)) =(2)/(8)=(1)/(4) =0.25`