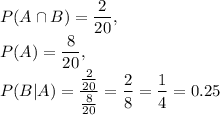Answer:
0.25
Explanation:
complete question:
Bart found 20 quadrilaterals in his classroom. He made a Venn diagram using the properties of the quadrilaterals, comparing those with four equal side lengths (E) and those with four right angles (R).
See attachment for the figure.
SOLUTION:
At Venn diagram there are 4 parts (20 pieces):
-> blue colored - quadrilaterals having four equal side lengths (3 pieces)
-> orange colored - quadrilaterals with four right angles (6 pieces)
-> blue and orange colored - quadrilaterals with four right angles and with four equal side lengths (2 pieces)
-> white colored - quadrilaterals without previous two properties (9 pieces).
Considering events:
A -> a randomly chosen quadrilateral has four right angles;
B -> a randomly chosen quadrilateral has four equal side lengths;
By using formula :
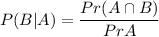 in order to find probability that a randomly selected quadrilateral with 4 right angles also has four equal side lengths:
in order to find probability that a randomly selected quadrilateral with 4 right angles also has four equal side lengths: