Question

A catalog sales company promises to deliver orders placed on the Internet within 3 days.​ Follow-up calls to a few randomly selected customers show that a 90​% confidence interval for the proportion of all orders that arrive on time is 85​%plus or minus4​%. What does this​ mean? Are the conclusions below​ correct? Explain. a )Between 81​% and 89​% of all orders arrive on time. b )90​% of all random samples of customers will show that 85​% of orders arrive on time. c )90​% of all random samples of customers will show that 81​% to 89​% of orders arrive on time. d )The company is 90​% sure that between 81​% and 89​% of the orders placed by the customers in this sample arrived on time.

Answer 1

The correct statement is (d).

Explanation:

The (1 - α)% confidence interval for the population proportion p is:

`CI=\hat p\pm z_(\alpha/2)* \sqrt{(\hat p(1-\hat p))/(n)}`

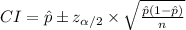
The 90​% confidence interval for the proportion of all orders that arrive on time is:

`CI=0.85\pm0.04\\CI=(0.81,\ 0.89)\\CI=(81\%,\ 89\%)`

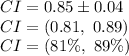
The (1 - α)% confidence interval for population parameter implies that there is a (1 - α) probability that the true value of the parameter is included in the interval.

Or, the (1 - α)% confidence interval for the parameter implies that there is (1 - α)% confidence or certainty that the true parameter value is contained in the interval.

The 90% confidence interval for the proportion of all orders that arrive on time, (81%, 89%), implies that there there is 0.90 probability that 81% to 89% of orders arrive on time.

Or, there is a 90% confidence that 81% to 89% of orders arrive on time.

Thus, the correct statement is (d).