Answer:
a)
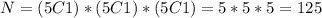
b)
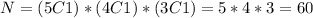
Explanation:
For this case our sample space is the 5 letters given:
![S= [F,G, H, I, J]](https://img.qammunity.org/2021/formulas/mathematics/college/oht4uvbx6mdhxmjkganv4j6bheac1v3dy4.png)
And we want to find the number of three letter words can be made from the sample space with some conditions
Part a
For this case the repetition is allowed so then each time we will have 5 possibilites in order to select one letter so if we use combinatories we have:
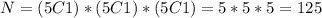
So then we will have 125 possible combinations of 3 words letters with the 5 provided
We need to remember that
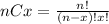
Part b
For this case the repetition is not allowed so then the possible number of possibilities are:
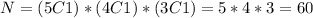
So then we will have 60 possible combinations of 3 words letters with the 5 provided