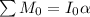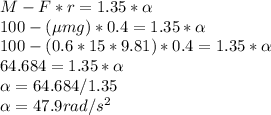Answer:
Angular acceleration of the wheel,
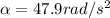
Acceleration of the wheel's center O, a = 5.886 m/s²
Step-by-step explanation:
The mass of the wheel, m = 15 kg
Let N = Normal reaction
μ = 0.6
Let the force acting horizontally be = F ( i.e the frictional force between the wheel and the plane)
Taking vertical equilibrium of forces: N - mg = 0
N - (15*9.81) = 0
N = 15 * 9.81
N = 147.15 N
F = ma ( where a is the horizontal acceleration)
F = 15a...........(1)
Taking horizontal equilibrium of forces: F -μN = 0
15a - 147.15(0.6) = 0
15a =88.29
a = 88.29/15
a = 5.886 m/s²
b) From the diagram, M = 100 Nm
Radius of the wheel, r = 0.4 m
Radius of gyration, k₀ = 300 mm = 0.3 m
The moment of inertia passing through the point O is given by:
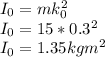
Taking moment about point O in the diagram with the horizontal force being F.