Answer:
a) The 95% confidence interval for the mean is (132.9, 140.9).
b) The 99.5% confidence interval for the mean is (131.1, 142.7).
c) Confidence level = 85.6%
Explanation:
a) We have to calculate a 95% confidence interval for the mean.
The population standard deviation is not known, so we have to estimate it from the sample standard deviation and use a t-students distribution to calculate the critical value.
The sample mean is M=136.9.
The sample size is N=123.
When σ is not known, s divided by the square root of N is used as an estimate of σM:

The t-value for a 95% confidence interval and 122 degrees of freedom is t=1.98.
The margin of error (MOE) can be calculated as:
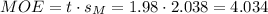
Then, the lower and upper bounds of the confidence interval are:
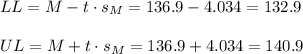
The 95% confidence interval for the mean is (132.9, 140.9).
b) We have to calculate a 99.5% confidence interval for the mean.
The t-value for a 100% confidence interval is t=2.859.
The margin of error (MOE) can be calculated as:

Then, the lower and upper bounds of the confidence interval are:

The 99.5% confidence interval for the mean is (131.1, 142.7).
c) We have a confidence interval that is (133.9, 139.9).
This corresponds to a margin of error of:
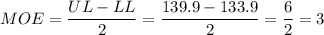
The critical value for this margin of error is:

This critical value of t=1.472 for 122 degrees of freedom corresponds to a confidence level of 85.6%. See picture attached.