Answer:
Step-by-step explanation:
Calculating the exit temperature for K = 1.4
The value of
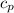 is determined via the expression:
is determined via the expression:
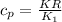
where ;
R = universal gas constant =
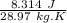
k = constant = 1.4
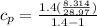
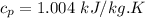
The derived expression from mass and energy rate balances reduce for the isothermal process of ideal gas is :
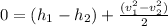 ------ equation(1)
------ equation(1)
we can rewrite the above equation as :
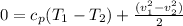
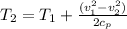
where:
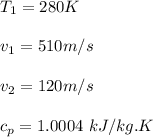
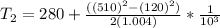
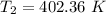
Thus, the exit temperature = 402.36 K
The exit pressure is determined by using the relation:
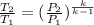
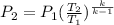

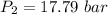
Therefore, the exit pressure is 17.79 bar