Question

What is the best first step in solving Negative 4 x + two-fifths greater-than StartFraction 5 over 10 EndFraction?

Add Two-fifths to both sides.
Subtract Two-fifths from both sides.
Multiply both sides by Negative 4 and reverse the inequality symbol.
Divide both sides by 10 and reverse the inequality symbol.

Answer 1

B - Subtract Two-fifths from both sides.

Answer 2

Correct option: Subtract Two-fifths from both sides.

Explanation:

The inequality is:

`-4x+(2)/(5)>(5)/(10)`

The best first step to solve the inequality will be to collect the like term on one side.

To do this, we must subtract
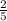`(2)/(5)` from both sides of the inequality.

`-4x+(2)/(5)-(2)/(5)>(5)/(10)-(2)/(5)\\\\-4x>(25-20)/(50)\\\\-4x>(1)/(10)`

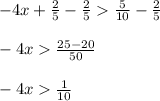
Now solve for x as follows:

`-4x>(1)/(10)\\\\x<(1)/(10)* (-1)/(4)\\\\x<-(1)/(40)`

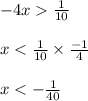
Thus, the value of x lies in the range
`x<-(1)/(40)`.