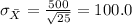Answer:

The mean for this case is given by:
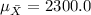
And the deviation would be:
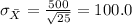
Explanation:
Using the following problem info since is incomplete the data: "The living spaces of all homes in a city have a mean of 2300 square feet and a standard deviation of 500 square feet. Let x be the mean living space for a random sample of 25 homes selected from this city. Find the mean and standard deviation of the sampling distribution of x."
We know the following info given:
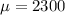 represent the mean for tehe living spaces of all homes in a city
represent the mean for tehe living spaces of all homes in a city
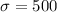 represent the population deviation for the data
represent the population deviation for the data
We select a sample size of n=25 so then this size is large enough in order to use the central limit theorem and we can use for the distribution of the sampel mean:

The mean for this case is given by:
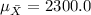
And the deviation would be: