Question

Find the least common multiple of 25k^4+200k^3+400k^2 and 15k^3+90k^2+120k answer in its factored form

Answer 1

75(k^2)(k+4)^2(k+2)

Explanation:

Answer 2

`75k(x+4)(x+2)`

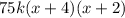
Explanation:

The first expression is

`25k^4+200k^3+400k^2`

First, we extract the greater common factor

`25k^(2)(k^(2)+8k+16 )`

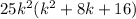
Second, we have the trinomial
`k^(2)+8k+16`

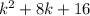
Notice that we need to find two number which product is 16 and which sum is 8, those numbers are 4 and 4.

So, the factors of the expression are

`25k^4+200k^3+400k^2=25k^(2) (x+4)(x+4)=25k^(2)(x+4)^(2)`

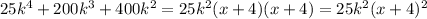
The second expression is

`15k^3+90k^2+120k`

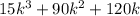
We use the same process.

Extract the greatest common factor

`15k(k^(2)+6k+8 )`

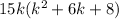
We solve the trinomial
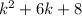`k^(2)+6k+8`. We need to find two numbers which product is 8 and which sum is 6, those numbers are 4 and 2.

`15k^3+90k^2+120k=15k(x+2)(x+4)`

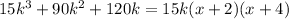
Now, the least common multiple is formed by factors that repeats in both expression.

Therefore, the least common multiple is
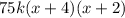`75k(x+4)(x+2)`, because the LCM between 25 and 15 is 75.