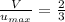Answer:
the volume flow rate per unit depth is:
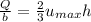
the ratio is :
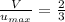
Step-by-step explanation:
From the question; the equations of the velocities profile in the system are:
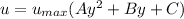 ----- equation (1)
----- equation (1)
The above boundary condition can now be written as :
At y= 0; u =0 ----- (a)
At y = h; u =0 -----(b)
At y =
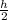 ; u =
; u =
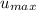 ------(c)
------(c)
where ;
A,B and C are constant
h = distance between two plates
u = velocity
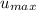 = maximum velocity
= maximum velocity
y = measured distance upward from the lower plate
Replacing the boundary condition in (a) into equation (1) ; we have:
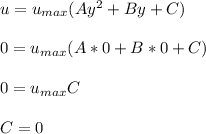
Replacing the boundary condition (b) in equation (1); we have:
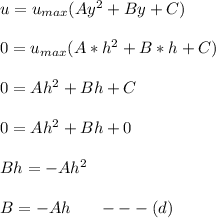
Replacing the boundary condition (c) in equation (1); we have:
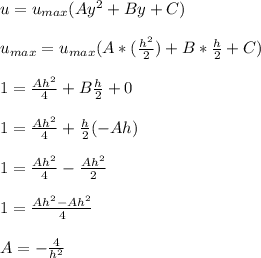
replacing
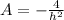 for A in (d); we get:
for A in (d); we get:
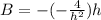
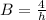
replacing the values of A, B and C into the velocity profile expression; we have:
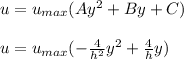
To determine the volume flow rate; we have:
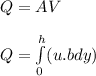
Replacing
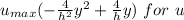
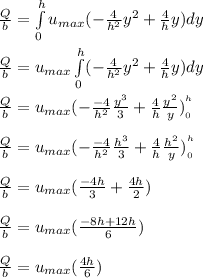
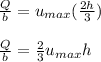
Thus; the volume flow rate per unit depth is:
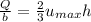
Consider the discharge ;
Q = VA
where :
A = bh
Q = Vbh
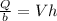
Also;
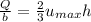
Then;
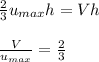
Thus; the ratio is :