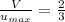Question

An incompressible fluid flows between two infinite stationary parallel plates. The velocity profile is given by u=umaxðAy2 + By+CÞ, where A, B, and C are constants and y is measured upward from the lower plate. The total gap width is h units. Use appropriate boundary conditions to express the magnitude and units of the constants in terms of h. Develop an expression for volume flow rate per unit depth and evaluate the ratio V=umax

Answer 1

the volume flow rate per unit depth is:

`(Q)/(b) = (2)/(3) u_(max) h`

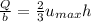
the ratio is :
`(V)/(u_(max))=(2)/(3)`

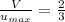
Step-by-step explanation:

From the question; the equations of the velocities profile in the system are:

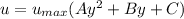`u = u_(max)(Ay^2+By+C)` ----- equation (1)

The above boundary condition can now be written as :

At y= 0; u =0 ----- (a)

At y = h; u =0 -----(b)

At y =
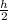`(h)/(2)` ; u =
`u_(max)` ------(c)

where ;

A,B and C are constant

h = distance between two plates

u = velocity

`u_(max)` = maximum velocity

y = measured distance upward from the lower plate

Replacing the boundary condition in (a) into equation (1) ; we have:

`u = u_(max)(Ay^2+By+C) \\ \\ 0 = u_(max)(A*0+B*0+C) \\ \\ 0=u_(max)C \\ \\ C= 0`

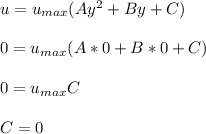
Replacing the boundary condition (b) in equation (1); we have:

`u = u_(max)(Ay^2+By+C) \\ \\ 0 = u_(max)(A*h^2+B*h+C) \\ \\ 0 = Ah^2 +Bh + C \\ \\ 0 = Ah^2 +Bh + 0 \\ \\ Bh = - Ah^2 \\ \\ B = - Ah \ \ \ \ \ --- (d)`

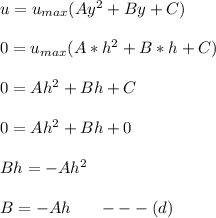
Replacing the boundary condition (c) in equation (1); we have:

`u = u_(max)(Ay^2+By+C) \\ \\ u_(max)= u_(max)(A*((h^2)/(2))+B*(h)/(2)+C) \\ \\ 1 = (Ah^2)/(4) +B (h)/(2) + 0 \\ \\ 1 = (Ah^2)/(4) + (h)/(2)(-Ah) \\ \\ 1= (Ah^2)/(4) - (Ah^2)/(2) \\ \\ 1 = (Ah^2 - Ah^2)/(4) \\ \\ A = -(4)/(h^2)`

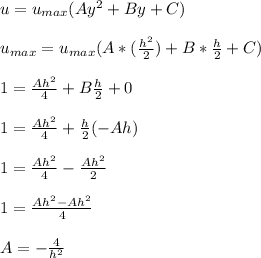
replacing
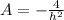`A = -(4)/(h^2)` for A in (d); we get:

`B = - ( -(4)/(h^2))h`
`B = (4)/(h)`

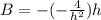
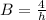
replacing the values of A, B and C into the velocity profile expression; we have:

`u = u_(max)(Ay^2+By+C) \\ \\ u = u_(max) (-(4)/(h^2)y^2+(4)/(h)y)`

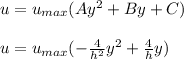
To determine the volume flow rate; we have:

`Q = AV \\ \\ Q= \int\limits^h_0 (u.bdy)`

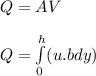
Replacing
`u_(max) (-(4)/(h^2)y^2+(4)/(h)y) \ for \ u`

`(Q)/(b) = \int\limits^h_0 u_(max)(-(4)/(h^2) y^2+(4)/(h)y)dy \\ \\ (Q)/(b) = u_(max) \int\limits^h_0 (-(4)/(h^2) y^2+(4)/(h)y)dy \\ \\ (Q)/(b) = u_(max) (-(-4)/(h^2)(y^3)/(3) +(4)/(h)(y^2)/(y))^ ^ h}}__0 }} \\ \\ (Q)/(b) =u_(max) (-(-4)/(h^2)(h^3)/(3) +(4)/(h)(h^2)/(y))^ ^ h}}__0 }} \\ \\ (Q)/(b) = u_(max)((-4h)/(3)+\frac{4h}2} ) \\ \\ (Q)/(b) = u_(max)((-8h+12h)/(6)) \\ \\ (Q)/(b) =u_(max)((4h)/(6))`

`(Q)/(b) = u_(max)((2h)/(3)) \\ \\ (Q)/(b) = (2)/(3) u_(max) h`

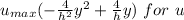
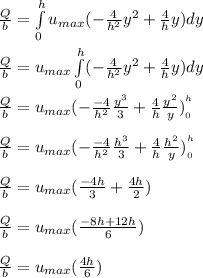
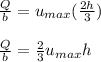
Thus; the volume flow rate per unit depth is:

`(Q)/(b) = (2)/(3) u_(max) h`

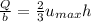
Consider the discharge ;

Q = VA

where :

A = bh

Q = Vbh

`(Q)/(b)= Vh`

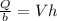
Also;
`(Q)/(b) = (2)/(3) u_(max) h`

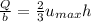
Then;

`(2)/(3) u_(max) h = Vh \\ \\ (V)/(u_(max))=(2)/(3)`

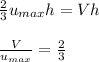
Thus; the ratio is :
`(V)/(u_(max))=(2)/(3)`