The question is incomplete! Complete question along with answer and step by step explanation is provided below.
Question:
Usually, in sports, we expect top athletes to get better over time. We expect future athletes to run faster, jump higher, throw farther. One thing has remained remarkably constant, however. The percent of free throws made by basketball players has stayed almost exactly the same for 50 years.1 For college basketball players, the percent is about 69% , while for players in the NBA (National Basketball Association) it is about 75% . (The percent in each group is also very similar between male and female basketball players.) In each case below, find the mean and standard deviation of the distribution of sample proportions of free throws made if we take random samples of the given size.
(a) Samples of 250 free throw shots in college basketball
mean _________
standard error __________
(b) Samples of 1000 free throw shots in college basketball
mean _________
standard error __________
(c) Samples of 250 free throw shots in the NBA
mean _________
standard error __________
(d) Samples of 1000 free throw shots in the NBA
mean _________
standard error __________
Answer:
(a)
mean = 0.69
standard error = 0.0292
(b)
mean = 0.69
standard error = 0.0146
(c)
mean = 0.75
standard error = 0.0274
(d)
mean = 0.75
standard error = 0.0137
Explanation:
We are given that the proportion of free throw shots made by college basketball players is
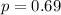
The proportion of free throw shots made by National Basketball Association players is
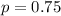
The mean of the distribution of sample proportions will be same as population mean that is
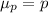
The standard deviation of the distribution of sample proportions is given by
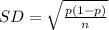
(a) Samples of 250 free throw shots in college basketball
Here we have n = 250 and p = 0.69
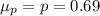
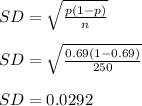
(b) Samples of 1000 free throw shots in college basketball
Here we have n = 1000 and p = 0.69
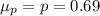
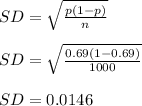
(c) Samples of 250 free throw shots in the NBA
Here we have n = 250 and p = 0.75
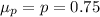
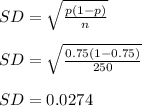
(d) Samples of 1000 free throw shots in the NBA
Here we have n = 1000 and p = 0.75
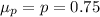
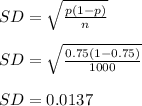
We can conclude that as the number of samples increases the standard deviation decreases.