Question

A random sample of 35 undergraduate students who completed two years of college were asked to take a basic mathematics test. The mean and standard deviation of their scores were 75.1 and 12.8, respectively. In a random sample of 50 students who only completed high school, the mean and standard deviation of the test scores were 72.1 and 14.6, respectively. Estimate with 90% confidence the difference in mean scores between the two groups of students. Assume the populations are approximately normal and σ1^2 ≠ σ2^2

Answer 1

`(75.1 -72.1) -1.66 \sqrt{(12.8^2)/(35) +(14.6^2)/(50)}= -1.96`

`(75.1 -72.1) +1.66 \sqrt{(12.8^2)/(35) +(14.6^2)/(50)}= 7.96`

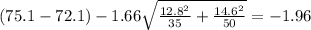
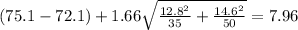
And the confidence interval would be given by:

`-1.96 \leq \mu_1 -\mu_2 \leq 7.96`

And since the confidence interval contains the value 0 we have enough evidence to conclude that we don't have significant differences between the two means at 10% of significance.

Explanation:

For this case we have the following info given :

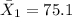`\bar X_1= 75.1` represent the sample mean for the scores of the undergraduate students

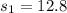`s_1 = 12.8` represent the standard deviation for the undergraduate students

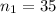`n_1 =35` the sample size for the undergraduate

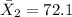`\bar X_2= 72.1` represent the sample mean for the scores of the high school students

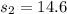`s_2 = 14.6` represent the standard deviation for the high school students

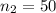`n_2 =50` the sample size for the high school

The confidence interval for the true difference of means is given by:

`(\bar X_1 -\bar X_2) \pm t_(\alpha/2) \sqrt{(s^2_1)/(n_1) +(s^2_2)/(n_2)}`

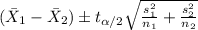
The degrees of freedom are given by:

`df=n_1 +n_2 -2= 35+50-2=83`

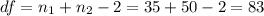
The confidence level is 90% and the significance level is
`\alpha=0.1` and
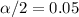`\alpha/2 =0.05` then the critical value would be:

`t_(\alpha/2)= 1.99`

And replacing the info we got:

`(75.1 -72.1) -1.66 \sqrt{(12.8^2)/(35) +(14.6^2)/(50)}= -1.96`

`(75.1 -72.1) +1.66 \sqrt{(12.8^2)/(35) +(14.6^2)/(50)}= 7.96`

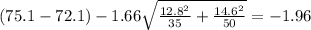
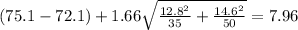
And the confidence interval would be given by:

`-1.96 \leq \mu_1 -\mu_2 \leq 7.96`

And since the confidence interval contains the value 0 we have enough evidence to conclude that we don't have significant differences between the two means at 10% of significance.