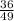Answer:
the ratio of the surface area of Pyramid A to Pyramid B is:
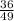
Explanation:
Given the information:
- Pyramid A : 648

- Pyramid B : 1,029

- Pyramid A and Pyramid B are similar
As we know that:
If two solids are similar, then the ratio of their volumes is equal to the cube
of the ratio of their corresponding linear measures.
<=>
 =
=
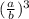 =
=
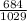 =
=
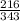
<=>
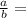

Howver, If two solids are similar, then the n ratio of their surface areas is equal to the square of the ratio of their corresponding linear measures
<=>
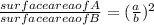
=
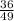
So the ratio of the surface area of Pyramid A to Pyramid B is: