Question

The scores on a math test are normally distributed with a mean of 78 and a standard deviation of 6. The test scores range from 0 to 100. Nineteen students had test scores between 72 and 90. Estimate the number of students who took the test.

Answer 1

The estimate for the number of students who took the test is 23.

Explanation:

The Empirical Rule states that, for a normally distributed random variable:

68% of the measures are within 1 standard deviation of the mean.

95% of the measures are within 2 standard deviation of the mean.

99.7% of the measures are within 3 standard deviations of the mean.

In this problem, we have that:

Mean = 78

Standard deviation = 6

Since the normal distribution is symmetric, 50% of the students had scores above the mean and 50% had scores below the mean.

Proportion of students who scored between 72 and 90:

72 = 78 - 6

So 72 is one standard deviation below the mean.

Of the 50% of the students who scored below the mean, 68% scored above 72.

90 = 78 + 2*6

So 90 is two standard deviations above the mean.

Of the 50% of the students who scored above the mean, 95% scored below 72.

Then

0.68*0.5 + 0.95*0.5 = 0.815

81.5% of the students scored between 72 and 90.

Nineteen students had test scores between 72 and 90. Estimate the number of students who took the test.

19 is 91.5% = 0.815 of the total number of students.

How much is 100% = 1?

19 - 0.815

x - 1

`0.815x = 19`

`x = (19)/(0.815)`

`x = 23.3`

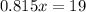
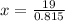
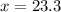
Rounding to the nearest whole number

The estimate for the number of students who took the test is 23.