Answer:
a) 67.03
b) 17.02
c) (50.01, 84.05)
Explanation:
Given that:
the male average expenditure
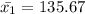
the female average expenditure
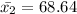
sample survey of the male
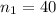
sample survey of the female
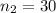
standard deviation of the male
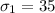
standard deviation of the female
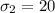
The Z-score is not given but it is meant to be =2.576
a) the point estimate of the difference between the population mean expenditure for males and the population mean expenditure for females is:
 = 135.67 - 68.64
= 135.67 - 68.64
= 67.03
b) At 99% confidence, the margin of error is calculated as:
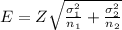
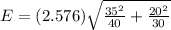
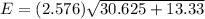
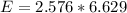
E = 17.02
c) the 99% confidence interval for the difference between the two population means is as follows:
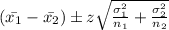
=
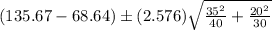
=
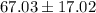
= (50.01, 84.05)