Question

The average expenditure on Valentine's Day was expected to be $100.89 (USA Today, February 13, 2006). Do male and female consumers differ in the amounts they spend? The average expenditure in a sample survey of 40 male consumers was $135.67, and the average expenditure in a sample survey of 30 female consumers was $68.64. Based on past surveys, the standard deviation for male consumers is assumed to be $35, and the standard deviation for female consumers is assumed to be $20.

a. What is the point estimate of the difference between the population mean expenditure for males and the population mean expenditure for females (to 2 decimals)? which is 67.03

b. At 99% confidence, what is the margin of error (to 2 decimals)?

c. Develop a 99% confidence interval for the difference between the two population means (to 2 decimals).

Answer 1

a) 67.03

b) 17.02

c) (50.01, 84.05)

Explanation:

Given that:

the male average expenditure
`\bar{x_1} = 135.67`

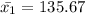
the female average expenditure
`\bar{x_2} = 68.64`

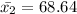
sample survey of the male
`n_1 = 40`

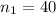
sample survey of the female
`n_2 = 30`

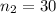
standard deviation of the male
`\sigma_1 = 35`

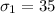
standard deviation of the female
`\sigma_2 = 20`

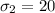
The Z-score is not given but it is meant to be =2.576

a) the point estimate of the difference between the population mean expenditure for males and the population mean expenditure for females is:

`\bar {x1} - \bar{x_2}` = 135.67 - 68.64

= 67.03

b) At 99% confidence, the margin of error is calculated as:

`E = Z \sqrt{(\sigma_1^2)/(n_1) + (\sigma_2^2)/(n_2) }`

`E = (2.576) \sqrt{(35^2)/(40) + (20^2)/(30) }`

`E = (2.576) √(30.625 + 13.33) }`

`E = 2.576*6.629`

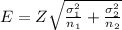
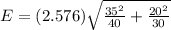
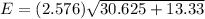
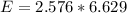
E = 17.02

c) the 99% confidence interval for the difference between the two population means is as follows:

`{( \bar {x_1} - \bar {x_2}) \pm z\sqrt{ (\sigma_1^2)/(n_1) + (\sigma_2^2)/(n_2) }`

=
`{( 135.67- 68.64}) \pm (2.576) \sqrt{ (35^2)/(40) + (20^2)/(30) }`

=
`67.03 \pm 17.02`

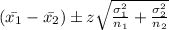
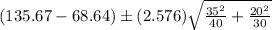
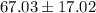
= (50.01, 84.05)