Question

Determine the decision criterion for rejecting the null hypothesis in the given hypothesis test; i.e., describe the values of the test statistic that would result in rejection of the null hypothesis. We wish to compare the means of two populations using paired observations. Suppose that the mean difference d bar = 3.125, sd = 2.911, and n = 8, and that you wish to test the following hypothesis at the 10% level of significance: H0 : µd = 0 against H1 : µd > 0.

What decision rule would you use? Group of answer choices

a).Reflect H0 if the test statistic is greater than -1.895 and less than 1.896.

b). Reject H0 if test statistic is greater than -1.895.

c). Reject H0 if test statistic is greater than 1.895.

d). Reject H0 if test statistic is less than 1.895

Answer 1

The critical value for this case can be calculated using the t distribution with 7 degrees of freedom and the critical value would be a value who accumulates 0.1 of the area in the right of the distribution and the best decision based on the possible options would be:

c). Reject H0 if test statistic is greater than 1.895.

Explanation:

The system of hypothesis for this case are:

Null hypothesis:
`\mu_d = 0`

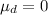
Alternative hypothesis:
`\mu_d >0`

The statistic for this case is given by:

`t=(\bar d -0)/((s_d)/(√(n)))=(3.125 -0)/((2.911)/(√(8)))=3.04`

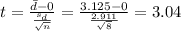
The degrees of freedom are given by:

`df=n-1=8-1=7`

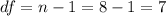
The p value for this case can be calculated from this probability:

`p_v =P(t_((7))>3.4) =0.0057`

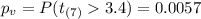
The critical value for this case can be calculated using the t distribution with 7 degrees of freedom and the critical value would be a value who accumulates 0.1 of the area in the right of the distribution and the best decision based on the possible options would be:

c). Reject H0 if test statistic is greater than 1.895.