Question

Please help me, i’m confused on this.

Answer 1

Answers A and B respectively

Explanation:

In the first pic, they are asking you for the value of the function at the points x = -1 and x = 5. Then you are asked to subtract your results. When the value of 'x' is -1, the 'y' value is 3. When the value of 'x' is 5, the 'y' value is -4. Therefore:

`f(-1)-f(5)=3-(-4)=7`

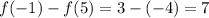
Answer A

For the second problem, they are saying that the line connecting points A and B is undefined. This means the slope is undefined along that line. An undefined slope is due to a zero in the denominator. Begin by taking the change in 'y' over the change in 'x' to get:

`(y_1-1)/(x_1+2) =m`

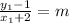
In order for our slope 'm' to be undefined, set the denominator to zero and see at what 'x' value this occurs at:

`x_1+2=0`

`x_1=-2`

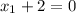
Then they say that the line connecting points C and D is zero. A zero slope would mean a zero in the numerator. Again, begin by taking the change in 'y' over the change in 'x' to get:

`(3-y_2)/(-5-x_2) =m`

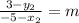
Set the numerator equal to zero to get:

`3-y_2=0`

`y_2=3`

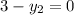
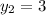
Answer B