Answer:
The values of x are 2.41 and -0.41
Explanation:
The given quadratic equation is
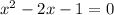
It is required to find the value of x form which the above equation is true. It means we need to solve the above equation for x. The solution of a quadratic equation
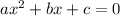 are :
are :
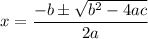
We have, a = 1, b = -2 and c = 1
Thus, plugging all values in formula, we get :
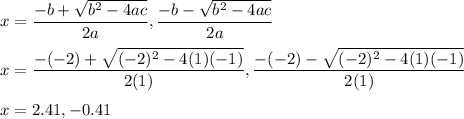
The values of x are 2.41 and -0.41