Answer:
The P-value is Less than 0.0005%.
Explanation:
We are given that at a branch office of the company, 350 people are polled and 125 indicate they are in favor of using a corporate American Express card.
A recent survey at the main corporate headquarters revealed that the 400 employees who responded to the survey indicated that 350 wanted to stay with the American Express Card.
Let
 = proportion of employees at the headquarters who want the American Express Card.
= proportion of employees at the headquarters who want the American Express Card.
 = proportion of employees at the branch office who want the American Express Card.
= proportion of employees at the branch office who want the American Express Card.
So, Null Hypothesis,
 :
:
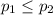 {means that the percentage of employees at the headquarters who want the American Express Card is smaller or equal to the percentage of employees at the branch office}
{means that the percentage of employees at the headquarters who want the American Express Card is smaller or equal to the percentage of employees at the branch office}
Alternate Hypothesis,
 :
:
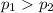 {means that the percentage of employees at the headquarters who want the American Express Card is greater than the percentage of employees at the branch office}
{means that the percentage of employees at the headquarters who want the American Express Card is greater than the percentage of employees at the branch office}
The test statistics that would be used here Two-sample z proportion statistics;
T.S. =
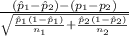 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of employees at the headquarters wanted to use the American Express Card =
= sample proportion of employees at the headquarters wanted to use the American Express Card =
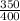 = 0.875
= 0.875
 = sample proportion of employees at the branch office wanted to use the American Express Card =
= sample proportion of employees at the branch office wanted to use the American Express Card =
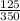 = 0.357
= 0.357
 = sample of people at the main corporate headquarters = 400
= sample of people at the main corporate headquarters = 400
 = sample of people at a branch office = 350
= sample of people at a branch office = 350
So, the test statistics =

= 16.99
The value of z test statistics is 16.99.
Now, P-value of the test statistics is given by;
P(Z > 16.99) = Less than 0.0005%